Log-likelihood calculator

To use this wizard, type in frequencies for one word and the corpus sizes and press the calculate button. Notes:
1. Please enter plain numbers without commas (or other non-numeric characters) as they will confuse the calculator!
2. The LL wizard shows a plus or minus symbol before the log-likelihood value to indicate overuse or underuse respectively in corpus 1 relative to corpus 2.
3. The log-likelihood value itself is always a positive number. However, my script compares relative frequencies between the two corpora in order to insert an indicator for '+' overuse and '-' underuse of corpus 1 relative to corpus 2.

How to calculate log likelihood

Log likelihood is calculated by constructing a contingency table as follows:

	Corpus 1	Corpus 2	Total
Frequency of word	a	b	a+b
Frequency of other words	c-a	d-b	c+d-a-b
Total	c	d	c+d

Note that the value 'c' corresponds to the number of words in corpus one, and 'd' corresponds to the number of words in corpus two (N values). The values 'a' and 'b' are called the observed values (O), whereas we need to calculate the expected values (E) according to the following formula:

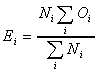
In our case N1 = c, and N2 = d. So, for this word, E1 = c*(a+b) / (c+d) and E2 = d*(a+b) / (c+d). The calculation for the expected values takes account of the size of the two corpora, so we do not need to normalize the figures before applying the formula. We can then calculate the log-likelihood value according to this formula:

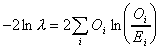
This equates to calculating log-likelihood G2 as follows: G2 = 2*((a*ln (a/E1)) + (b*ln (b/E2)))

Note: (thanks to Chris Brew) To form the log-likelihood, we calculate the sum over terms of the form x*ln(x/E). For strictly positive x it is easy to compute these terms, while if x is zero ln(x/E) will be negative infinity. However the limit of x*ln(x) as x goes to zero is still zero, so when summing we can just ignore cells where x = 0. Calculating ln(0) returns an error in, for example, MSExcel and the C-maths library.

The higher the G2 value, the more significant is the difference between two frequency scores. For these tables, a G2 of 3.8 or higher is significant at the level of p < 0.05 and a G2 of 6.6 or higher is significant at p < 0.01.

95th percentile; 5% level; p < 0.05; critical value = 3.84
99th percentile; 1% level; p < 0.01; critical value = 6.63
99.9th percentile; 0.1% level; p < 0.001; critical value = 10.83
99.99th percentile; 0.01% level; p < 0.0001; critical value = 15.13

References

For a detailed comparison of the log-likelihood and chi-squared statistics, see
Rayson P., Berridge D. and Francis B. (2004). Extending the Cochran rule for the comparison of word frequencies between corpora. In Volume II of Purnelle G., Fairon C., Dister A. (eds.) Le poids des mots: Proceedings of the 7th International Conference on Statistical analysis of textual data (JADT 2004), Louvain-la-Neuve, Belgium, March 10-12, 2004, Presses universitaires de Louvain, pp. 926 - 936. ISBN 2-930344-50-4.

The log-likelihood test can be used for corpus comparison. See
Rayson, P. and Garside, R. (2000). Comparing corpora using frequency profiling. In proceedings of the workshop on Comparing Corpora, held in conjunction with the 38th annual meeting of the Association for Computational Linguistics (ACL 2000). 1-8 October 2000, Hong Kong, pp. 1 - 6.

For a more detailed review of various statistics, see:
Rayson, P. (2003). Matrix: A statistical method and software tool for linguistic analysis through corpus comparison. Ph.D. thesis, Lancaster University.

I've made a spreadsheet incorporating the log-likelihood calculation: LL.xls. This would be useful if you want to calculate a large number of results from pre-existing datasets.

The chi-square distribution calculator (Stat Trek) makes it easy to compute cumulative probabilities, based on the chi-square statistic.

The Institute of Phonetic Sciences in Amsterdam, have a similar calculator.

Also see Dunning, Ted. (1993). Accurate Methods for the Statistics of Surprise and Coincidence. Computational Linguistics, Volume 19, number 1, pp. 61-74. (postscript, pdf)

If you have technical problems please get in touch with Paul Rayson
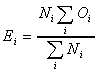
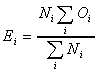
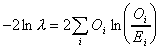